Let’s say someone got you a gift and they handed you this huge wrapped-up box that required all your strength to hold. You then start to unwrap this gift and soon realise that inside this gift-wrapped box is another...gift-wrapped box…you continue to unwrap this smaller box and once you’re done, you realise there’s another even smaller gift-wrapped box inside it. This goes on for three more boxes (getting smaller and smaller) until you finally reach the gift (imagine that ideal item you’ve been longing to have or own for ages). That’s recursion! You’re solving a bigger problem by breaking it down into smaller problems until you reach the simplest one.

We just described the concept of recursion using a metaphor of unwrapping nested gift boxes. The initial large wrapped box represents the original problem. The act of unwrapping it to reveal another gift-wrapped box inside represents a recursive function calling itself to solve a smaller sub-problem. The process continues until a base case is reached, which is symbolised by the smaller gift box that contains the desired gift. In the context of C programming, it represents a recursive function that calls itself repeatedly until it reaches a base case.

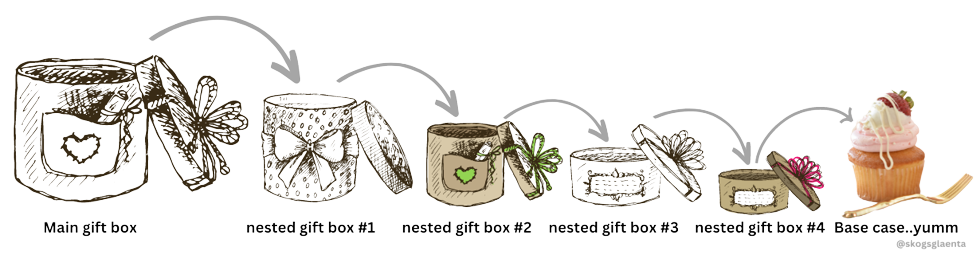
The image above depicts an illustration of Recursion.

Introduction

Recursion is a fundamental concept in Computer Science and programming that allows a function or method to call itself within its own definition. In this post, we will explore what recursion is, how to implement it, and when it should and should not be used.

What is Recursion?

Recursion is a programming technique that involves a function or method calling itself within its own definition. The idea behind recursion is to break a problem down into smaller and smaller sub-problems until they are simple enough to solve. Each time the function is called, it works on a smaller and simpler version of the original problem until the base case is reached.

The base case is the condition in which the function does not call itself again and returns a value. The base case is essential because, without it, the function would continue to call itself indefinitely, resulting in an infinite loop and eventually crashing the program.

How to implement Recursion:

To implement recursion in a program, you need to define a function or method that calls itself within its own definition. To gain a better understanding of recursion, suppose we wanted to calculate the factorial of a number using recursion.

Note ✍🏼: The factorial of a number is the product of all positive integers less than or equal to that number.

#include <stdio.h>
#include "main.h"

/**
* main - Entry point of the program
* 
* Description: Recursive function to calculate the factorial of a number
* Return: nothing
*/
int factorial(int n)
{

    int i;   

    /* Base case: when n is 0 or 1, return 1*/
    if (n == 0 || n == 1)
    {
        return (1);
    }
    else
    {
         /* Recursive case: multiply n with factorial(n-1)*/
         return (n * factorial(n-1));

    }
}

int main()
{
   int num = 5;
   int result = factorial(num);

   printf("The factorial of %d is %d\n", num, result);

   return (0);
}

What does all this mean? — Let's walk through the above function step-by-step:

1. First, include the standard libraries #include <stdio.h> required to use built-in functions like printf

2. Then we include the function description, sting the name and purpose of the function as well as any parameters in use

3. We declare a recursive function called factorial that takes an integer n as a parameter and return an integer

4. Inside the factorial function, we have the base case. If n is 0 or 1, we return 1 because the factorial of 0 or 1 is 1

5. If n is not 0 or 1, we have a recursive case. We then calculate the factorial by multiplying n with the factorial of n-1. To do this, we call the factorial function again with the parameter n-1.

6. In the main function, we initialise a variable number to 5 (the number whose factorial we want to calculate).

7. We call the factorial function with num as the argument and store the result in the variable result.

8. Finally, we use printf to display the result.

When the program is run, it will (hopefully ) calculate the factorial of 5 using recursion and print the result as “The factorial of 5 is 120 “ (if not, then we need to keep calm and debug 🐞).

When to use Recursion:

Recursion is an excellent tool for solving problems that can be broken down into smaller and simpler sub-problems. Here are some situations in which recursion can be helpful:

1. Sorting Algorithms: some searching algorithms such as quicksort and mergesort use recursion to divide the problem into smaller sub-problem.

2. Search Algorithms: some search algorithms such as binary search and depth-first search use recursion to explore a problem space.

3. Mathematical Problems: recursive solutions are often used in mathematical problems such as the Fibonacci sequence or calculating factorials.

When not to use Recursion:

Recursion as said previously can be a powerful tool, but it is not always the best solution to a problem. Here are some situations in which recursion should not be used:

1. Large Data Sets: recursion can cause stack overflow errors if too many function calls are made. this can be a problem when dealing with large data sets.

2. Deeply Nested Recursion: deeply nested recursion can be difficult to understand and debug, leading to errors and performance issues.

3. Overhead: as mentioned earlier, each function call requires additional memory, which can lead to performance issues when dealing with large data sets.

Conclusion

While recursion can be a powerful technique, it’s important to consider the problem’s characteristics, input size, language limitations, and performance requirements before deciding to use recursion or opt for an iterative approach. It’s important to have a base case that terminates the recursion. Otherwise, the function will keep calling itself indefinitely, leading to an infinite loop (which isn’t a bad thing if you love gifts...but at some point, you’ll want to get to the base case sooner than later 🤭).

Thanks for reading. Happy Coding!